The mxfda package contains tools for analyzing spatial
single-cell data, including multiplex imaging and spatial
transcriptomics, using methods from functional data analysis. Analyses
for this package are executed and stored using an S4 object of class
mxFDA. This vignette outlines how to set up an
mxFDA object from spatial single cell imaging data, how to
calculate spatial summary functions, and exploratory data analysis and
visualization of these spatial summary functions. Details on how to
perform downstream analysis and feature extraction using functional
principal component analysis can be found in the separate vignette
vignette("mx_fpca"). To perform functional regression on
spatial summary functions from multiplex imaging data, see
vignette("mx_funreg").
VectraPolarisData
Examples in this package use data adapted from the VectraPolarisData package on Bioconductor’s ExperimentHub. This package contains data from two multiplex imaging experiments conducted at the University of Colorado Anschutz Medical Campus. A shortcourse on single-cell multiplex imaging using these data is available here.
Data has been preprocessed and stored directly in the
mxfda package. Available datasets are
ovarian_FDA and lung_df. This vignette will
focus on the lung_df dataset, which contains a subset of 50
subjects from a multiplex imaging study of non-small cell lung carcinoma
described in Johnson et al. (2021). Each
subject has 3-5 multiplex images, which come from different regions of
interest (ROIs) in the tumor. Each ROI will be considered a “sample”
when constructing the mxfda object. We load the lung
cancer data below.
data(lung_df)Setting up the mxFDA object
The central object used with the mxfda package is the
mxFDA object. These objects are created with
make_mxfda() and hold everything from the raw spatial data
to fit functional data models using derived spatial summary functions.
To save space on large samples, the metadata is kept separately from the
spatial data and when needed, is exported and merged together. Slots in
the mxFDA object are designated as follows:
-
Metadata- stores sample specific traits that may be used as covariates when fitting models -
Spatial- a data frame of cell level information (x and y spatial coordinates, phenotype, etc.) that can be used to calculate spatial summary functions -
subject_key- a character string for the column in the metadata that denotes the unique subject ID -
sample_key- a character string for the column in the metadata that denotes the unique sample ID. Note that there may be multiple samples per subject, and this ID links the metadata and spatial data for each multiplex image sample -
univariate_summariesandbivariate_summaries- lists of spatial summary functions either imported withadd_summary_function()or calculated withextract_summary_functions() -
functional_pca- list of results from functional principle component analysis -
functional_mpca- list of results from multilevel functional principle component analysis -
functional_cox- list of functional cox models that have been fit
Make mxFDAobject
Using the ?lung_df in the mxfda package,
columns with repeated data pertaining to the sample-level information
are extracted and stored in a data frame called clinical
while the cell-level information is kept in a long data frame
(make_mxfda() also accepts cell-level information as a list
of data frames). The spatial parameter in the make_mxfda()
function can be left blank if using a spatial metric derived from
external functions. The final 2 parameters for the ?lung_df
mxFDA object are the subject_key and the
sample_key. The sample_key is a column name
that appears both in the metadata and spatial
and denotes unique samples while the subject_key is a
column name in metadata that ties the samples to metadata;
if the data contains one sample per subject then sample_key
and subject_key is a 1:1, but if multiple samples per
subject, subject_id will be repeated.
clinical = lung_df %>%
select(image_id, patient_id, patientImage_id, gender, age, survival_days, survival_status, stage) %>%
distinct()
spatial = lung_df %>%
select(-image_id, -gender, -age, -survival_days, -survival_status, -stage)
mxFDAobject = make_mxfda(metadata = clinical,
spatial = spatial,
subject_key = "patient_id",
sample_key = "patientImage_id")Note that the object created has class mxFDA.
class(mxFDAobject)
#> [1] "mxFDA"
#> attr(,"package")
#> [1] "mxfda"Spatial summary functions based on point processes
The mxfda package provides methods for analyzing spatial relationships between cell types in single cell imaging data based on point process theory. The location of cells in image samples are treated as following a point process, realizations of a point process are called “point patterns”, and point process models seek to understand correlations in the spatial distributions of cells. Under the assumption that the rate of a cell is constant over an entire region of interest a point pattern will exhibit complete spatial randomness (CSR), and it is often of interest to model whether cells deviate from CSR either through clustering or repulsion. When the rate of a cell is not constant, this CSR assumption is violated and to estimate CSR it is recommended to use permutations (see C. Wilson et al. (2022) for explanation).
Spatial summary statistics can be calculated to quantify the clustering and co-occurrence of cells in a circular region with a particular radius r. Typically univariate (one cell type) or bivariate (two cell types) summary statistics are reported, and inference is obtained by comparing the observed spatial summary statistic to that obtained under CSR. A popular quantity is Ripley’s K(r), which studies the number of neighbors to a particular point within radius r, and has univariate and bivariate implementations in the spatstat package (Baddeley, Rubak, and Turner (2015)). Ripley’s K is characterized by clustering or repulsion depending on whether it is above or below the theoretical value of \(\pi r^2\). Other spatial summary statistics analyze the distance to a neighbor, and can be interpreted as probabilities of observing a particular cell type within a radius r. One of these metrics, G(r), or the nearest neighbor distance distribution, is the cumulative distribution function of an exponential random variable. More detailed overviews of spatial summary functions for multiplex imaging data are provided in C. M. Wilson et al. (2021) and Wrobel, Harris, and Vandekar (2023).
Univariate summary functions
Below we calculate univariate Ripley’s K to summarize the spatial
relationship among immune cells in each image. The mxfda
package accomplishes this with the function
extract_summary_functions(). Either univariate or bivariate
can be calculated with this function depending on the choice supplied to
the extract_func argument. To calculate a univariate
spatial summary we supply univariate to the
extract_func argument. The summary function that is
calculated depends on the function supplied to summary_fun
which is one of Kest(), Gest(), or
Lest() from the spatstat.explore package
(Kcross(), Gcross(), or Lcross()
for bivariate methods). Other options include supplying a vector of
radius values through r_vec, and the a specific edge
correction (see Baddeley, Rubak, and Turner
(2015)). We calculate the K function across a range of radii from
0 to 100 and use the isotropic (“iso”) edge correction. See Baddeley, Rubak, and Turner (2015) for more
details on edge corrections for Ripley’s K and nearest neighbor G.
Options permute_CSR and permutations can be
used if interested in using a measure of the sample-specific CSR instead
of the theoretical, the column specified with markvar just
needs to contain 1 level more than used for summary_func (2
levels for univariate and 3 levels for bivariate) otherwise falls back
to theoretical.
mxFDAobject = extract_summary_functions(mxFDAobject,
extract_func = univariate,
summary_func = Kest,
r_vec = seq(0, 100, by = 1),
edge_correction = "iso",
markvar = "immune",
mark1 = "immune")
#> Using Theoretical Complete Spatial Randomness for Ripley's K
#> ■■■■■■■■■■■■■■■■■■■ 60% | ETA: 2sRunning this code will calculate univariate Ripley’s K function to
measure spatial clustering of immune cells for each sample, and will
store these spatial summary functions in the
univariate_summaries slot of the mxFDAobject.
To access this slot and view the extracted summary functions, type:
mxFDAobject@univariate_summaries$Kest
#> # A tibble: 24,947 × 6
#> patientImage_id r sumfun csr fundiff `immune cells`
#> <chr> <dbl> <dbl> <dbl> <dbl> <int>
#> 1 2_1 0 0 0 0 6
#> 2 2_1 1 0 3.14 -3.14 6
#> 3 2_1 2 0 12.6 -12.6 6
#> 4 2_1 3 0 28.3 -28.3 6
#> 5 2_1 4 0 50.3 -50.3 6
#> 6 2_1 5 0 78.5 -78.5 6
#> 7 2_1 6 0 113. -113. 6
#> 8 2_1 7 0 154. -154. 6
#> 9 2_1 8 0 201. -201. 6
#> 10 2_1 9 0 254. -254. 6
#> # ℹ 24,937 more rowsNote that the summaries are returned as a dataframe. The variable
sumfun is the estimated summary function value,
csr is the theoretical value under complete spatial
randomness, and fundiff =
sumfun-csr describes the “degree of clustering
beyond what is expected due to chance; in downstream analysis we will
use the fundiff covariate.
Plotting the mxFDA object
mxfda has S4 methods for visualization implemented via
the plot() function (see ?plot.mxFDA for
details). The first argument is the mxFDA object followed
by a few options that depend on what plot output is desired. Here, we
want to plot the univariate summary that we just calculated, which was
the K function. By passing in what = 'uni k', the plot
function will extract the univariate K results. We also need to tell
plot() what column is the y-axis which can be
'sumfun' for the observed value, 'csr' for the
theoretical value of complete spatial randomness (CSR), or
'fundiff' which is the difference between the observed K
measure and the theoretical CSR. The output of plot() is a
ggplot2 object which can then be easily added
to/manipulated as any ggplot plot would.
NOTE: These are the columns when calculating using the
extract_summary_function() of mxfda but if
summary data is added from elsewhere with
add_summary_function() then those column names will have to
be used.
plot(mxFDAobject, y = "fundiff", what = "uni k") +
geom_hline(yintercept = 0, color = "red", linetype = 2)
Bivariate summary functions
The extract_summary_functions() function can also be
used to extract bivariate summaries comparing spatial clustering of 2
cell types. We will look at relationship between T-cells and
macrophages. There are a few images that have fewer than 5 T-cells or
macrophages, which makes estimation of spatial summary functions less
stable for those images. To look at T-cells and macrophages, the data
phenotypes and cell locations have to be in long format so we first
create a variable with the cell types ('phenotype') from
the lung_df.
lung_df = lung_df %>%
mutate(phenotype = case_when(phenotype_cd8 == "CD8+" ~ "T-cell",
phenotype_cd14 == "CD14+" ~ "macrophage",
TRUE ~ "other"),
phenotype = factor(phenotype))We then recreate the mxFDAobject
spatial = lung_df %>%
select(-image_id, -gender, -age, -survival_days, -survival_status, -stage)
mxFDAobject = make_mxfda(metadata = clinical,
spatial = spatial,
subject_key = "patient_id",
sample_key = "patientImage_id")Now we calculate the bivariate G function, but can replace
Gcross() with Lcross() or
Kcross() to estimate the L or K bivariate functions
instead. The argument markvar takes the variable that we
created above called 'phenotype', and the 2 cell types that
we are interested in calculating the bivariate G for are
'T-cell' and 'macrophage' so we provide them
to mark1 and mark2, respectively.
mxFDAobject = extract_summary_functions(mxFDAobject,
summary_func = Gcross,
extract_func = bivariate,
r_vec = seq(0, 100, by = 1),
edge_correction = "rs",
markvar = "phenotype",
mark1 = "T-cell",
mark2 = "macrophage")
#> Using Theoretical Complete Spatial Randomness for Bivariate Ripley's K - L TransformPlotting bivariate G
Just like with the univariate plots, we can use the
plot() function to plot our mxFDA object
results. The what now is 'bi g',
'bivar g', or 'bivariate g'.
plot(mxFDAobject, y = "fundiff", what = "bi g") +
geom_hline(yintercept = 0, color = "red", linetype = 2)
#> Warning: Removed 712 rows containing missing values or values outside the scale range
#> (`geom_line()`).
Exploring the S4 object
Another useful function is ?summary.mxFDA which feeds
into the summary() method. Either typing the name of the
object or wrapping it in the summary function will provide information
like the number of subjects, samples, if spatial summary functions have
been calculated, and functional data analyses that have been run.
mxFDAobject
#> mxFDA Object:
#> Subjects: 50
#> Samples: 247
#> Has spatial data
#> Univariate Summaries: None
#> Bivariate Summaries: Gcross
#> FPCs not yet calculated
#> MFPCs not yet calculated
#> FCMs not yet calculated
#> MFCMs not yet calculated
#> Scalar on Functional Regression not calculatedSpatialTIME
Sometimes other summary functions or normalizations are run outside of the mxfda package but the end goal is to still run functional data analysis. Other packages, such as spatialTIME (Creed et al. (2021)) provide methods for fast calculation of functions in spatstat with permutation estimates of complete spatial randomness that are more robust than theoretical CSR estimates, especially when tissue samples have holes that violate the assumption of a homogeneous point pattern (see C. Wilson et al. (2022)). Lets look at how to perform the estimation of univariate nearest neighbor G with spatialTIME.
The central object of spatialTIME is the
mIF object, that contains a list of spatial data frames, a
data frame of sample-level summaries, and a data frame for the metadata
(‘clinical’). From creating the mxFDA object, we have a
spatial data frame and the clinical data, now we have to convert them
into something that works with spatialTIME. The steps below
will be:
- convert positive/negative to 1/0 integers
- identify which columns in the spatial data frame are cell types
- convert spatial data frame to a list, where each element is a unique sample
- create a summary data frame from the spatial list for the number and proportion of positive cells for each phenotype
#Step 1
spatialTIME_spatial_df = spatial %>%
select(-phenotype) %>%
mutate(across(phenotype_ck:phenotype_cd4, ~ ifelse(grepl("\\+", .x), 1, 0))) %>%
relocate(patientImage_id, .before = 1)
#Step 2
cell_types = colnames(spatialTIME_spatial_df) %>% grep("phenotype", ., value = TRUE)
#Step 3
spatial_list = split(spatialTIME_spatial_df, spatial$patientImage_id)
#Step 4
summary_data = lapply(spatial_list, function(df){
df %>%
#group by sample ID to maintain ID column
group_by(patient_id, patientImage_id) %>%
#find number of positive
reframe(across(!!cell_types, ~ sum(.x)),
`Total Cells` = n()) %>%
#calculate proportion
mutate(across(!!cell_types, ~.x/`Total Cells` * 100, .names = "{.col} %"))
}) %>%
#bind the rows together
do.call(bind_rows, .)With the spatial list, clinical, and summary data the
mIF object can be constructed. For best computation
efficiency, use >v1.3.4.
library(spatialTIME)
#> spatialTIME version:
#> 1.3.4.5
#> If using for publication, please cite our manuscript:
#> https://doi.org/10.1093/bioinformatics/btab757
#make mif
mif = create_mif(clinical_data = clinical,
sample_data = summary_data,
spatial_list = spatial_list[1:50],
patient_id = "patient_id",
sample_id = "patientImage_id")Deriving spatial metrics with the mIF object is really
easy but does take some time. Will only do 10 permutations here to
estimate the complete spatial randomness measure of nearest neighbor G
and a reduced sampling, or 'rs', edge correction. To make
the run faster, will look at only cytotoxic T cells (CD8+) and helper T
cells (CD4+).
mif = NN_G(mif, mnames = cell_types[c(2, 6)],
r_range = 0:100, num_permutations = 10,
edge_correction = "rs", keep_perm_dis = FALSE,
workers = 1, overwrite = TRUE, xloc = "x", yloc = "y")With spatialTIME, all cell types (markers) are added to
the data frame. We can visualize both CD8+ and CD4+ with ggplot.
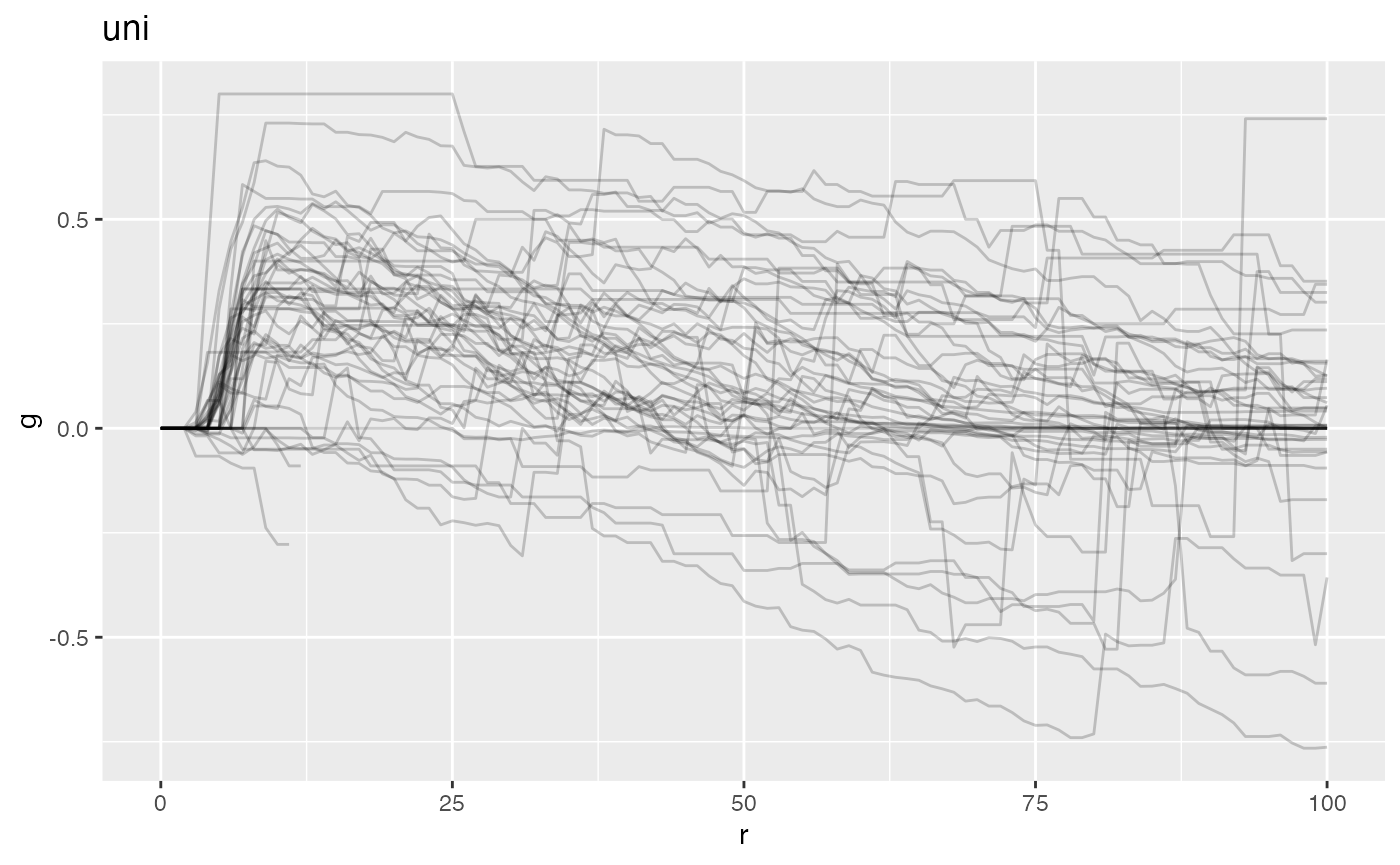
mif$derived$univariate_NN %>%
ggplot() +
geom_line(aes(x = r, y = `Degree of Clustering Permutation`, color = patientImage_id), alpha = 0.4) +
facet_grid(~Marker) +
theme(legend.position = "none")
#> Warning: Removed 1086 rows containing missing values or values outside the scale range
#> (`geom_line()`).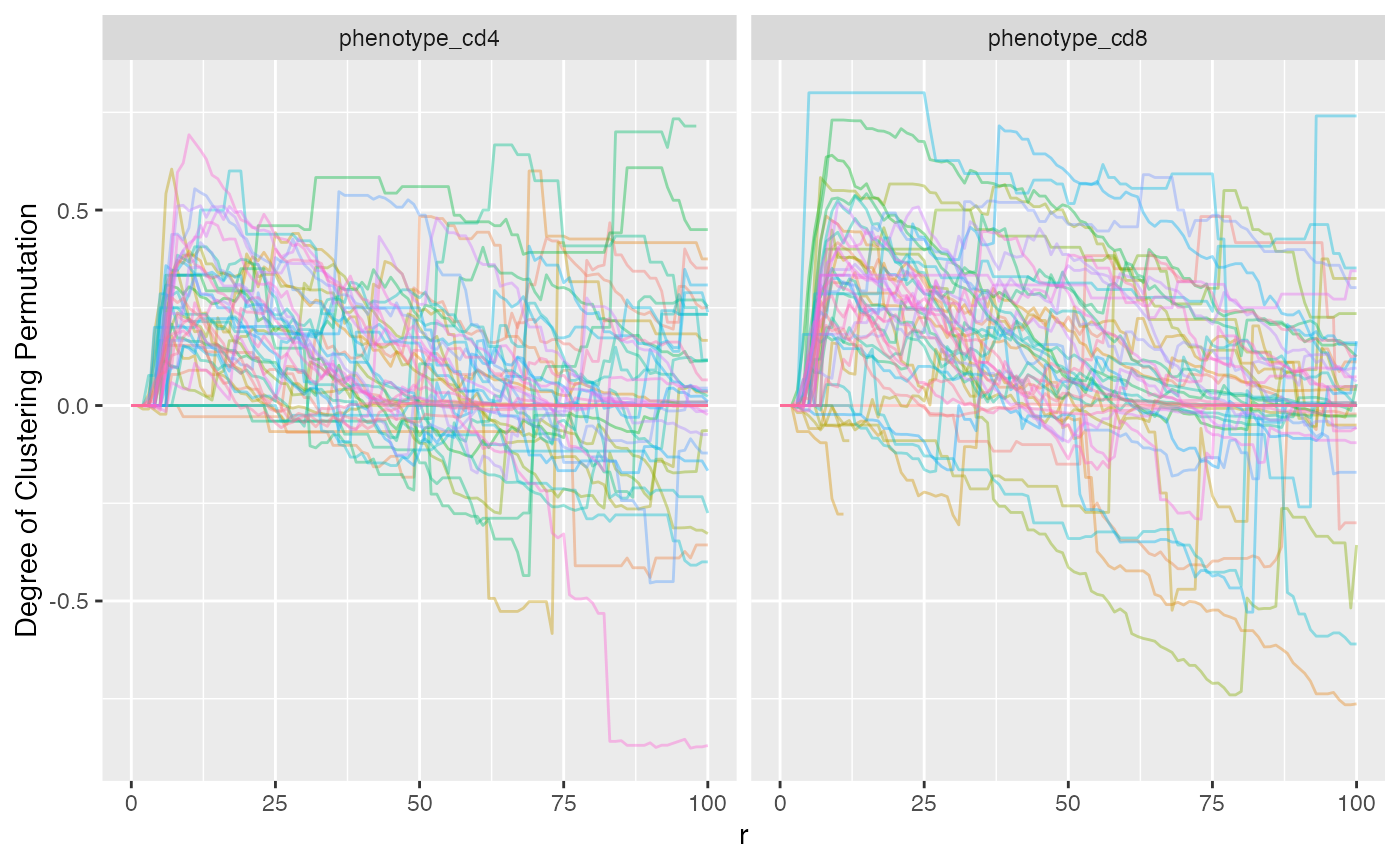
Exporting the spatial summary function data from the mIF
object is the same as accessing the list object. However, we need to
make sure that the data that we use with the mxFDA object
contains only a single cell types results. This is to make sure that
when modeling we aren’t mixing up different cells. Below is the
extraction and filtering of the new univariate G results and keeping
only the cytotoxic T cell results.
With the derived univariate nearest neighbor G for CD8+, it can be
added to an mxFDA object with
add_summary_function(). To show this, first will create a
new mxFDA object with an empty spatial slot then add the
new summary function results.
#make mxFDA object
mxFDA_spatialTIME = make_mxfda(metadata = clinical,
spatial = NULL,
subject_key = "patient_id",
sample_key = "patientImage_id")
#add summary data
mxFDA_spatialTIME = add_summary_function(mxFDAobject,
summary_function_data = uni_g,
metric = "uni g")Can now use the mxfda plot method with the new data and
continue with analyses as would be done if using the internal
extract_summary_function().
plot(mxFDA_spatialTIME, y = "Degree of Clustering Permutation", what = "uni g")
#> Warning: Removed 480 rows containing missing values or values outside the scale range
#> (`geom_line()`).